Week of November 18 - 22

Figure above:  A step-by-step animation of the construction of a regular hexagon using compass and straightedge, given by Euclid's Elements, Book IV, Proposition 15. (from Wikipedia)

No homework on Thursday: Come out and support Doc Nesin in her recovery from cancer at the pasta dinner served by Governor Baldacci at LMS.

6th grade - See the note below about Friday's class.

Working on Shapes and Designs this week.

       Tuesday - work as assigned (see below) 

The 7th grade had FUN with your designs! On Thursday, we will look at what the 7th grade did with your designs :)

assignments: 

LP - poster for sum of interior angles, then read this page on exterior angles and then this page on exterior angles and do questions 1 through 8 at the bottom of the page, and then Geometry > F.3 Exterior Angle Theorem and Geometry > 

G.4 Review: interior and exterior angles of polygons

DH - math story, then read this page on exterior angles and then this page on exterior angles and do questions 1 through 8 at the bottom of the page and then Geometry > F.3 Exterior Angle Theorem and Geometry > 
G.4 Review: interior and exterior angles of polygons;

TW, GH - - read this page on exterior angles and then this page on exterior angles and do questions 1 through 8 at the bottom of the page and then Geometry > F.3 Exterior Angle Theorem and Geometry > 
G.4 Review: interior and exterior angles of polygons. 

NL - and Mrs. LB's other students if you finish your work for her - read this page on exterior angles and then this page on exterior angles and do questions 1 through 8 at the bottom of the page and then Geometry > F.3 Exterior Angle Theorem and Geometry > 
G.4 Review: interior and exterior angles of polygons. 


       Wednesday - everybody (6th grade) has pre-assessments for Trimester 2, so we will     not meet.

       Thursday - class as usual

       Friday - Work on your RADAR assignment. (The word RADAR is a link to where you need to go.) Read all of the sections on radar. Then, write to me an email and in it tell me three things you learned about radar. IF you have time, LP - do your POSTER, DH - do your story, GH / TW / NL - work on this in IXL and related sections if you have time.

For CR and TMcC: Keep working on your IXL! I am very pleased by your motivation. Look at these videos on multiplying and dividing fractions. (These are YouTube videos, so you may not be able to access them at school. If not, do them at home for homework.)

Have a great weekend!

Math note:  For interior angles

In a regular polygon of N sides the sum of the interior angles is 

(N - 2)180 deg. 

The measure of each angle is 

180 deg - (N-2)180 

         N

Algebra - 

Chapter 4 is an EXTREMELY important chapter. 

You MUST take your time and get these concepts. 

Tuesday  - EK and ZF - read pages 215 - 218 and do questions 1, 2, 3, 4, 5, 6, & 9 on page 219. (This is what we did in class after you left.) 

All - CAREFULLY do these questions:

p. 219 #11 (Look at how the book gives you this solution.Do your other problems like this.) 

p. 219 # 12, 16, 20, 23, 24, 25, 26, 28, 30
p. 220 # 36, 37* (worked out solution - look at how the book does it), 38

      

      Wednesday - class as usual 

      
Thursday - class as usual. You have practiced graphing a linear equation using a table of values. Today we will graph a linear equation using intercepts. 

For ZF and EK who have extended math in the morning: 

Add these words to the vocabulary of your reference section -

- translation, transformation, reflection, stretch and shrink (p. 213)
- linear function (p. 217)
- discrete function (p. 223)
- continuous function (p. 223)

Then read examples 1 through 5 in Section 4.3. Come to class prepared to explain these examples.

If time remains, work in  IXL - graphing functions
and IXL -completing a function table
and IXL - writing rules for function tables
     

 Friday - EH and KD, please look at the work assigned to your classmates ZF and EK yesterday. Do the same: Add these words to the vocabulary of your reference section -

- translation, transformation, reflection, stretch and shrink (p. 213)
- linear function (p. 217)
- discrete function (p. 223)
- continuous function (p. 223)

Then read examples 1 through 5 in Section 4.3. Come to class prepared to explain these examples.

If time remains, work in  IXL - graphing functions
and IXL -completing a function table
and IXL - writing rules for function tables 

ALL - On Friday (and over the weekend) practice these questions on Graphing using Intercepts in Section 4.3:

p. 229-231:   q. 1, 3, 4, 7, 10, 13, 21, 24, 27, 29, 32, 35, 37, 38 - 40, 41, 42, 43, 47

On Monday, we will start Section 4.4, Finding Slope and Rate of Change

Geometry - 

      Tuesday - work as assigned
      Wednesday - NO CLASS - work as assigned
      Thursday - class as usual 
      
Friday -  We have been working our way through Chapter 5, a very important chapter. We have looked at centroid and orthocenter. I think we have been using centroid interchangeably with incenter, though:

The centroid is the intersection of the three medians of the triangle.

       


The incenter is the intersection of the angle 
bisectors of the triangle.

       

Note the difference: The orthocenter is the intersection of the triangle's 
altitudes.

       



We haven't talked about this, but it's worth noting: 
The circumcenter is the center of the circumscribed circle (the 
intersection of the perpendicular bisectors of the three sides).

    

And most interestingly: 

The Euler line of a triangle is the line which passes through the 
orthocenter, circumcenter, and centroid of the triangle.  

    

(Images from http://mathforum.org/library/drmath/view/57665.html)

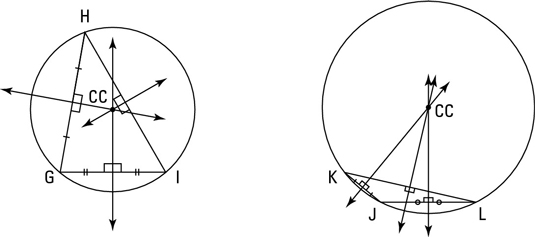
And more:

Finding the incenter

You find a triangle’s incenter at the intersection of the triangle’s three angle bisectors. This location gives the incenter an interesting property: The incenter is equally far away from the triangle’s three sides. No other point has this quality. Incenters, like centroids, are always inside their triangles.

The above figure shows two triangles with their incenters and inscribed circles, or incircles (circles drawn inside the triangles so the circles barely touch the sides of each triangle). The incenters are the centers of the incircles. (Don’t talk about this “in” stuff too much if you want to be in with the in-crowd.)

Finding the circumcenter

You find a triangle’s circumcenter at the intersection of the perpendicular bisectors of the triangle’s sides. This location gives the circumcenter an interesting property: the circumcenter is equally far away from the triangle’s three vertices.

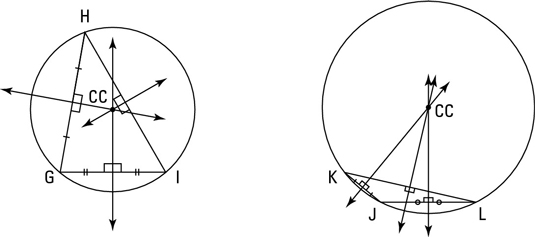
The above figure shows two triangles with their circumcenters and circumscribed circles, orcircumcircles (circles drawn around the triangles so that the circles go through each triangle’s vertices). The circumcenters are the centers of the circumcircles.

You can see in the above figure that, unlike centroids and incenters, a circumcenter is sometimes outside the triangle. The circumcenter is

• Inside all acute triangles
• Outside all obtuse triangles
• On all right triangles (at the midpoint of the hypotenuse)
  
  
  In math class on Friday, read through Sections 5.1 to 5.3 if you need the refresher. Then, work through these problems in your book (if you haven't don't them already):
  
  
  p.314 (ha! pi page!) q. 19, 21, 22, 24, 25, 27
  p. 317  q. 1, 2 a. b. c., 6
  
  
  Over the weekend, work on Section 5.4 - Using Means and Altitudes
  
  
  On Monday, we will look ahead to Sections 5.5 (Use Inequalities in a Triangle) and 5.6  (Inequalities in Two Triangles and Indirect Proof). You will practice at home Monday and Tuesday, and then work on a Chapter Review / Exit Test over the Holiday. I will give you the materials you need on Monday.